TECHNOLOGIE
Un nouveau modèle quantique de la diffraction
Un scientifique de l’Irfu a publié dans la Physical Review A un article qui présente un modèle de diffraction basé sur le concept de mesure quantique. Ce modèle constitue une approche nouvelle car l’amplitude de l’onde diffractée est habituellement calculée par les méthodes classiques de l’optique ondulatoire.
Plusieurs effets spécifiques de l’aspect quantique du modèle sont prédits dont trois peuvent faire l’objet de tests expérimentaux: un amortissement typique de l’intensité lumineuse aux grands angles de diffraction, un facteur angulaire différent de celui des théories classiques et un paramètre caractéristique d’un lien entre la polarisation et l’impulsion des photons diffractés. Des expériences réalisées à l’IRAMIS dans les prochains mois permettront d’effectuer la mesure simultanée de l’impulsion et de la polarisation des photons détectés et ainsi de valider ou non le modèle proposé.
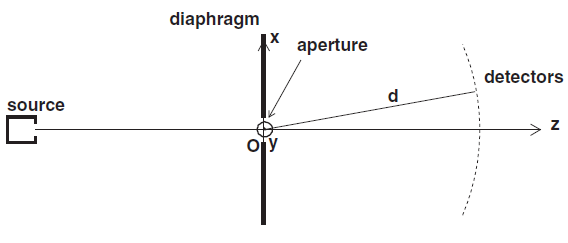
Le phénomène de diffraction peut être observé lorsqu’une onde rencontre des obstacles matériels, par exemple un diaphragme dont on peut régler l’ouverture (figure 1).

Figure 1: dispositif expérimental de diffraction d’une onde par un diaphragme.L’onde issue de la source et arrivant sur l’ouverture du diaphragme peut être considérée comme une onde plane dont la direction de propagation est celle de l’axe Oz (appelée direction longitudinale). La diffraction se produit lors du passage de l’onde par l’ouverture. L’onde plane incidente devient une onde diffractée qui se propage désormais dans plusieurs directions autour de l’axe Oz avec une intensité différente pour chaque direction. La valeur de cette intensité en fonction de la direction (distribution angulaire) dépend de la forme de l’ouverture et de la longueur d’onde.
En optique ondulatoire classique, l’amplitude de l’onde diffractée peut être calculée en appliquant le principe de Huygens-Fresnel selon lequel le front d’onde situé à l’ouverture est un ensemble de sources secondaires émettant des ondelettes sphériques vers la région où se trouvent les détecteurs. La somme de ces ondelettes, qui interfèrent entre elles, est égale à l’onde diffractée.

Figure 2: exemple d’ouverture 3D (coupe dans le plan x,z) avec les fonctions de filtrage transverse et longitudinale.
En mécanique quantique, l’onde est associée à une particule, par exemple le photon dans le cas de la lumière. Le calcul effectué en optique ondulatoire à partir du principe de Huygens-Fresnel est équivalent à un calcul direct de la fonction d’onde de la particule mais sans calcul préalable de son état quantique.
Le modèle présenté dans l’article récemment publié part des principes de base de la mécanique quantique pour calculer cet état quantique et en déduire ensuite la fonction d’onde. Il considère la diffraction par un diaphragme comme la conséquence d’une mesure de la position de la particule lorsqu’elle passe par l’ouverture et exprime l’état qui résulte de cette mesure de position.
Cette dernière comprend la mesure des coordonnées transverses (x,y), avec les incertitudes Δx et Δy correspondant à la taille de l’ouverture, mais aussi une mesure de z puisque la particule traverse alors le plan du diaphragme pour lequel z = 0. Or, en vertu de la mécanique quantique, cette mesure de z s’effectue avec une incertitude Δz qui est en général non nulle. La mesure de position provoque donc une localisation temporaire de la fonction d’onde dans un volume constituant une sorte d’ouverture tridimensionnelle (3D). La notion de fonction de filtrage est utilisée pour représenter la zone de localisation relative à chaque coordonnée (figure 2). L’ouverture 3D est formée à partir de l’ouverture 2D transverse utilisée en optique ondulatoire et d’une ouverture 1D longitudinale. L’absence de bord matériel dans la direction longitudinale entraîne que la fonction de filtrage associée n’est pas nécessairement une fonction créneau comme dans le cas des coordonnées transverses.
Trois effets spécifiques du caractère quantique du modèle peuvent faire l’objet de mesures:
1 – Principe de Huygens-Fresnel multi-fronts d’onde
La prise en compte de la coordonnée longitudinale dans le cadre d’une ouverture 3D entraîne que l’émission des ondelettes impliquées dans le principe de Huygens-Fresnel ne se produit pas à partir d’un seul front d’onde mais de plusieurs fronts voisins. La largeur Δz de la distribution de ces fronts d’onde est un paramètre du modèle et peut être ajustée aux données de mesure de l’intensité de l’onde diffractée en fonction de l’angle de diffraction. La figure 3 présente deux prédictions du modèle quantique (correspondant à deux valeurs de Δz) et les prédictions des trois théories classiques les plus connues de l’optique ondulatoire (Fresnel-Kirchhoff et Rayleigh-Sommerfeld 1 et 2) pour un cas de diffraction de photons par une fente rectangulaire.
Des différences significatives entre les prédictions apparaissent aux grands angles de diffraction, une région pour laquelle des mesures expérimentales précises manquent. Le modèle quantique prédit un amortissement typique de l’intensité dans cette région, d’autant plus important que Δz est grand (courbe QM2). Une étude expérimentale du principe de Huygens-Fresnel est donc envisageable.

Figure 3: comparaison entre cinq prédictions théoriques de l’intensité relative pour un cas de diffraction de photons: trois prédictions de l’optique ondulatoire (WO) correspondant aux théories de Fresnel-Kirchhoff (FK) et de Rayleigh-Sommerfeld (RS1 et RS2) et deux prédictions du modèle quantique (QM1 et QM2) où la fonction de filtrage longitudinal est une gaussienne (GLF). Le 0 correspond au principe de Huygens-Fresnel à un seul front d’onde. Dans le modèle quantique, en plus de l’amortissement lié à la valeur de Δz, la décroissance de l’intensité en fonction de l’angle de diffraction dépend d’un facteur angulaire différent des facteurs d’obliquité (ou d’inclinaison) des théories de l’optique ondulatoire. Ce facteur décrit de façon plausible la décroissance de l’intensité jusqu’à zéro à la limite angulaire de 90° (courbes QM1 et QM2) contrairement aux courbes FK et RS2 pour lesquelles la valeur à 90° est en général non nulle. La courbe RS1 décroît jusqu’à zéro mais différemment des courbes QM.
3 – Polarisation
La mesure de position modifie les états de polarisation des particules. Dans le cas de photons incidents dans un état pur de polarisation elliptique, le modèle quantique prédit que les axes de l’ellipse peuvent subir une rotation qui dépend du transfert d’impulsion entre la particule et le diaphragme et par suite de l’angle de diffraction. L’angle de cette rotation est un paramètre du modèle. Il peut être ajusté aux données de mesures de polarisation des photons détectés.
Des expériences pour tester le modèle quantique sont actuellement en cours de préparation à l’IRAMIS/SPEC/LEPO (F. Charra, L. Douillard, C. Fiorini, S. Vassant). Le montage expérimental permettra d’atteindre un angle maximum de 75° et d’effectuer la mesure simultanée de l’impulsion et de la polarisation des photons détectés.
Références
B. Fabbro, “Position measurement and the Huygens-Fresnel principle: A quantum model of Fraunhofer diffraction for polarized pure states”, Phys. Rev. A 107, 033706 (2023) (https://doi.org/10.1103/PhysRevA.107.033706).